Remember those scatterplots you graphed in your math class, painstakingly plotting points representing data sets? Remember the feeling of bewilderment when tasked with drawing a line that somehow represented the overall trend of those dots? Well, that line you drew is called a line of best fit, and it’s a powerful tool for understanding and predicting relationships between data. It’s more than just a line; it’s a doorway to understanding how variables interact, and its applications are as diverse as the data sets it can analyze.
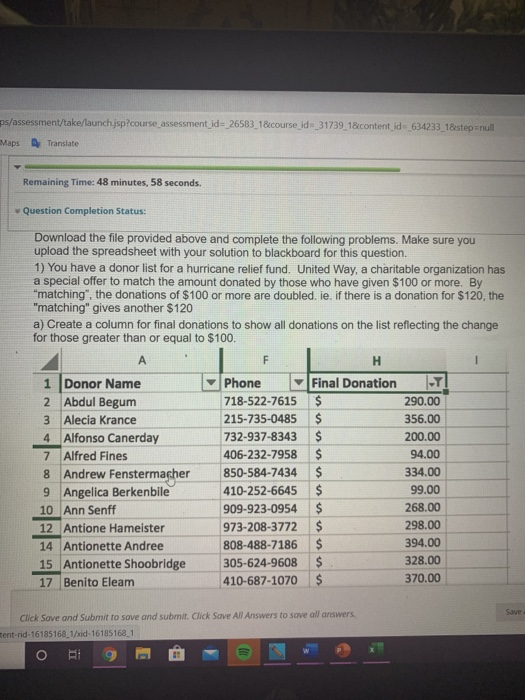
Image: www.chegg.com
In this exploration, we’ll delve deeper into the world of lines of best fit. We’ll uncover the secrets behind their calculation, the crucial role they play in various fields, and their application to real-world scenarios. We’ll also provide you with a set of practice problems with detailed solutions, helping you master the art of analyzing lines of best fit and putting your knowledge to the test. Let’s embark on this journey together, unlocking the power of lines of best fit, one problem at a time.
The Essence of Lines of Best Fit: A Visual Representation of Trends
A line of best fit is a straight line that best approximates the relationship between two variables on a scatter plot. This line acts as a visual representation of the trend shown by the data points. Determining the line of best fit is a crucial step in understanding the underlying relationship between the two variables. This line reveals the average rate of change between the two variables, allowing you to interpret the relationship and predict future outcomes.
Mastering the Art: Methods for Finding the Line of Best Fit
While it’s possible to visually estimate a line of best fit by eye, more precise methods are readily available. The most commonly used approach is the method of least squares, which minimizes the sum of squared differences between the actual data points and the predicted values on the line. This sophisticated method ensures that the line of best fit captures the overall trend of the data as accurately as possible.
Practical Applications: Illuminating the Real World
Lines of best fit are not confined to the theoretical realm of mathematics. They are extensively used across diverse fields, providing insights and predictions that impact decision-making. Here are just a few examples:
Image: www.chegg.com
1. Economic Growth: Predicting Financial Trends
Economists use lines of best fit to analyze economic indicators, such as GDP growth, inflation rates, and investment trends. By plotting data points representing these variables over time, economists can draw lines of best fit and use their slopes and intercepts to forecast future economic performance.
2. Environmental Science: Understanding Climate Change
Scientists utilize lines of best fit to analyze data sets related to climate change. By plotting average temperatures, sea levels, and greenhouse gas concentrations over time, they can identify trends and predict future climate patterns, facilitating informed strategies to address climate change.
3. Medical Research: Unveiling Disease Patterns
In medical research, lines of best fit are instrumental in analyzing the relationship between patient characteristics, such as age and lifestyle factors, and disease incidence and progression. By examining these relationships, researchers can develop better disease prevention and treatment strategies.
4. Business Analytics: Optimizing Operations
Business analysts rely on lines of best fit to analyze sales data, customer behavior, and market trends. By understanding these relationships, they can optimize pricing strategies, predict demand, and make data-driven decisions to improve business performance.
Applying Your Skills: Practice Problems with Answer Keys
Now it’s time to put your newfound knowledge to the test. Let’s work through some practice problems that will solidify your understanding of lines of best fit and their applications. Each problem will be accompanied by a detailed solution, ensuring that you learn from your practice and build confidence in your analytical skills.
Practice Problem 1: Estimating the Cost of a New Car
Scenario: You are interested in buying a new car, but you want to have a good idea of the price range before you start your search. You gather data on the prices of several similar cars, plotting the price against the number of miles driven on the cars. The data points suggest a linear relationship between price and mileage. Your goal is to find the line of best fit and use it to estimate the price of a new car with similar features but with zero mileage.
Data:
| Miles Driven (x) | Price (y) |
|---|---|
| 10,000 | $22,000 |
| 20,000 | $19,000 |
| 30,000 | $16,000 |
| 40,000 | $13,000 |
| 50,000 | $10,000 |
Solution:
-
Plot the data: Plot the mileage (x) on the horizontal axis and the price (y) on the vertical axis. The resulting scatter plot should show a downward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points. The line should be close to as many points as possible, with roughly the same number of points above and below the line.
-
Calculate the slope: The slope of the line of best fit represents the rate of change in price for each mile driven. To calculate the slope, choose two points on the line (not necessarily data points) and use the formula:
Slope (m) = (Change in price) / (Change in mileage)
For example, let’s choose the points (10,000, $22,000) and (40,000, $13,000). The slope is then:
m = ($13,000 – $22,000) / (40,000 – 10,000) = -$0.30 per mile
-
Calculate the y-intercept: The y-intercept represents the predicted price of a car with zero mileage. To find the y-intercept, use the point-slope form of a linear equation:
y – y1 = m(x – x1)
Using the point (10,000, $22,000) and the slope m = -$0.30, we have:
y – $22,000 = -$0.30(x – 10,000)
To find the y-intercept, set x = 0:
y – $22,000 = -$0.30(0 – 10,000)
y = $25,000 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = -$0.30x + $25,000
-
Estimate the price of a new car: To estimate the price of a new car (zero mileage), plug x = 0 into the equation:
y = -$0.30(0) + $25,000 = $25,000
Therefore, the estimated price of a new car with similar features is $25,000.
Practice Problem 2: Predicting Student Performance
Scenario: You are a teacher, and you want to see if there is a relationship between the number of hours students study each week and their exam scores. You collect data on the study hours and exam scores of your students.
Data:
| Study Hours (x) | Exam Score (y) |
|---|---|
| 5 | 70 |
| 10 | 80 |
| 15 | 90 |
| 20 | 95 |
| 25 | 100 |
Solution:
-
Plot the data: Plot the study hours (x) on the horizontal axis and the exam scores (y) on the vertical axis. The scatter plot should show an upward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points.
-
Calculate the slope: Choose two points on the line and use the slope formula:
Slope (m) = (Change in exam score) / (Change in study hours)
For example, let’s choose the points (5, 70) and (20, 95). The slope is then:
m = (95 – 70) / (20 – 5) = 1.67
-
Calculate the y-intercept: Use the point-slope form of a linear equation with the point (5, 70) and the slope m = 1.67:
y – 70 = 1.67(x – 5)
To find the y-intercept, set x = 0:
y – 70 = 1.67(0 – 5)
y = 61.65 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = 1.67x + 61.65
-
Predict the exam score for a student who studies for 12 hours:
y = 1.67(12) + 61.65 = 81.79
Thus, a student who studies for 12 hours per week is predicted to get an exam score of approximately 81.79.
Practice Problem 3: Investigating the Relationship Between Temperature and Cricket Chirps
Scenario: Scientists have observed that crickets chirp at a rate that is directly related to the surrounding temperature. You collect data on the number of chirps per minute and the corresponding air temperature.
Data:
| Chirps per minute (x) | Temperature (y) |
|---|---|
| 10 | 60 |
| 15 | 65 |
| 20 | 70 |
| 25 | 75 |
| 30 | 80 |
Solution:
-
Plot the data: Plot the chirps per minute (x) on the horizontal axis and the temperature (y) on the vertical axis. The scatter plot should show an upward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points.
-
Calculate the slope: Choose two points on the line and use the slope formula:
Slope (m) = (Change in temperature) / (Change in chirps per minute)
For example, let’s choose the points (10, 60) and (30, 80). The slope is then:
m = (80 – 60) / (30 – 10) = 1
-
Calculate the y-intercept: Use the point-slope form of a linear equation with the point (10, 60) and the slope m = 1:
y – 60 = 1(x – 10)
To find the y-intercept, set x = 0:
y – 60 = 1(0 – 10)
y = 50 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = x + 50
-
Predict the temperature if the crickets chirp at 22 chirps per minute:
y = 22 + 50 = 72
Thus, if the crickets chirp at a rate of 22 chirps per minute, the predicted temperature is 72 degrees.
Practice Problem 4: Analyzing the Relationship Between Exercise and Weight Loss
Scenario: You are interested in understanding the relationship between the amount of exercise a person gets and their weight loss. You collect data on the number of hours of exercise per week and the weight loss in pounds for several individuals.
Data:
| Exercise Hours (x) | Weight Loss (y) |
|---|---|
| 2 | 3 |
| 4 | 5 |
| 6 | 7 |
| 8 | 9 |
| 10 | 11 |
Solution:
-
Plot the data: Plot the exercise hours (x) on the horizontal axis and the weight loss (y) on the vertical axis. The scatter plot should show an upward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points.
-
Calculate the slope: Choose two points on the line and use the slope formula:
Slope (m) = (Change in weight loss) / (Change in exercise hours)
For example, let’s choose the points (2, 3) and (10, 11). The slope is then:
m = (11 – 3) / (10 – 2) = 1
-
Calculate the y-intercept: Use the point-slope form of a linear equation with the point (2, 3) and the slope m = 1:
y – 3 = 1(x – 2)
To find the y-intercept, set x = 0:
y – 3 = 1(0 – 2)
y = 1 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = x + 1
-
Predict the weight loss for a person who exercises for 7 hours per week:
y = 7 + 1 = 8
Therefore, a person who exercises for 7 hours per week is predicted to lose approximately 8 pounds.
Practice Problem 5: Exploring the Relationship Between Age and Salary
Scenario: You are interested in understanding the relationship between age and salary for employees in a certain industry. You collect data on the ages and salaries of a sample of employees.
Data:
| Age (x) | Salary (y) |
|---|---|
| 25 | $50,000 |
| 30 | $60,000 |
| 35 | $70,000 |
| 40 | $80,000 |
| 45 | $90,000 |
Solution:
-
Plot the data: Plot the age (x) on the horizontal axis and the salary (y) on the vertical axis. The scatter plot should show an upward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points.
-
Calculate the slope: Choose two points on the line and use the slope formula:
Slope (m) = (Change in salary) / (Change in age)
For example, let’s choose the points (25, $50,000) and (45, $90,000). The slope is then:
m = ($90,000 – $50,000) / (45 – 25) = $2,000 per year
-
Calculate the y-intercept: Use the point-slope form of a linear equation with the point (25, $50,000) and the slope m = $2,000:
y – $50,000 = $2,000(x – 25)
To find the y-intercept, set x = 0:
y – $50,000 = $2,000(0 – 25)
y = $0 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = $2,000x
-
Predict the salary for an employee who is 38 years old:
y = $2,000(38) = $76,000
Thus, an employee who is 38 years old is predicted to have a salary of approximately $76,000.
Practice Problem 6: Analyzing the Relationship Between Advertising Spending and Sales
Scenario: A company is interested in understanding the relationship between its advertising spending and its sales. It collects data on its advertising expenditures and corresponding sales figures.
Data:
| Advertising Spending (x) | Sales (y) |
|---|---|
| $10,000 | $50,000 |
| $20,000 | $70,000 |
| $30,000 | $90,000 |
| $40,000 | $110,000 |
| $50,000 | $130,000 |
Solution:
-
Plot the data: Plot the advertising spending (x) on the horizontal axis and the sales (y) on the vertical axis. The scatter plot should show an upward linear trend.
-
Draw a line of best fit: Visually estimate a line that best represents the general trend of the data points.
-
Calculate the slope: Choose two points on the line and use the slope formula:
Slope (m) = (Change in sales) / (Change in advertising spending)
For example, let’s choose the points ($10,000, $50,000) and ($50,000, $130,000). The slope is then:
m = ($130,000 – $50,000) / ($50,000 – $10,000) = $2 per dollar of advertising
-
Calculate the y-intercept: Use the point-slope form of a linear equation with the point ($10,000, $50,000) and the slope m = $2:
y – $50,000 = $2(x – $10,000)
To find the y-intercept, set x = 0:
y – $50,000 = $2(0 – $10,000)
y = $30,000 -
Line of Best Fit Equation: The equation of the line of best fit is:
y = $2x + $30,000
-
Predict the sales if the company spends $35,000 on advertising:
y = $2($35,000) + $30,000 = $100,000
Therefore, if the company spends $35,000 on advertising, it is predicted to generate approximately $100,000 in sales.
3-6 Additional Practice Analyzing Lines Of Best Fit Answer Key
Harnessing the Power of Lines of Best Fit: Mastering Analysis and Prediction
Our exploration of lines of best fit has taken us on a journey from visualizing trends in data to predicting real-world outcomes. We’ve learned that these lines are more than just mere mathematical constructs. They are tools that empower us to analyze relationships, interpret trends, and make informed decisions.
Lines of best fit are a powerful testament to the transformative power of data analysis. They illuminate trends that might otherwise remain hidden, allowing us to understand the world around us more deeply. Whether you are a student, a professional, or simply someone who wants to make data-driven decisions, mastering the art of analyzing lines of best fit is a valuable skill that can unlock a world of understanding and prediction.





