Have you ever stared at a right triangle, its sides and angles whispering secrets, and wished you had a magic key to unlock them? Well, the magic key exists, and it’s called trigonometry! This fascinating branch of mathematics empowers us to unravel the mysteries of right triangles, finding missing sides and angles with precision. Whether you’re a student facing a trigonometry exam or simply curious about the elegant relationships within these shapes, join us as we explore the wonders of right triangle trigonometry.
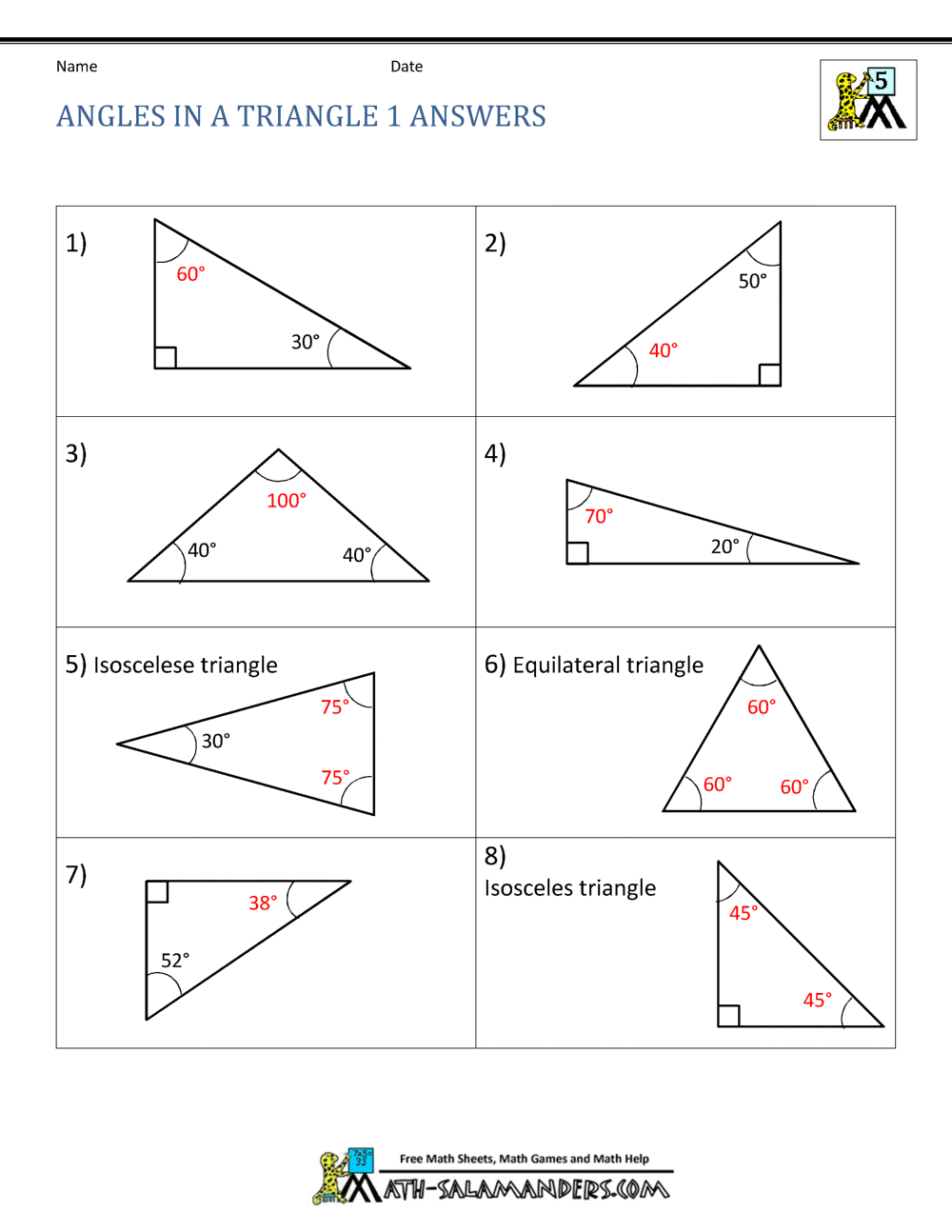
Image: www.pdfprof.com
Imagine you’re a surveyor standing on a hill, gazing at a distant tower. You need to determine the tower’s height, but you only have a compass, a measuring tape, and a bit of trigonometry knowledge. With some clever calculations, you can use the angles and known distances to solve the mystery! Right triangle trigonometry doesn’t just stop with towers, though. It’s a fundamental tool in fields like architecture, engineering, physics, and even astronomy. This article will equip you with the understanding and tools to navigate the intriguing world of right triangles and their secrets.
Understanding the Basics: SOH CAH TOA
The foundation of right triangle trigonometry is built on three fundamental ratios: sine, cosine, and tangent, which are often remembered with the mnemonic acronym SOH CAH TOA.
-
SOH stands for Sine = Opposite / Hypotenuse.
-
CAH stands for Cosine = Adjacent / Hypotenuse.
-
TOA stands for Tangent = Opposite / Adjacent.
Let’s break down these ratios and understand their role in solving right triangle mysteries.
1. Sine (SOH):
The sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse (the longest side). A simple way to remember this is to visualize the sine as the “opposite” side over the “hypotenuse”.
2. Cosine (CAH):
The cosine of an angle is the ratio of the length of the side adjacent to the angle (the side next to the angle) to the length of the hypotenuse. Think of cosine as the “adjacent” side over the “hypotenuse.”
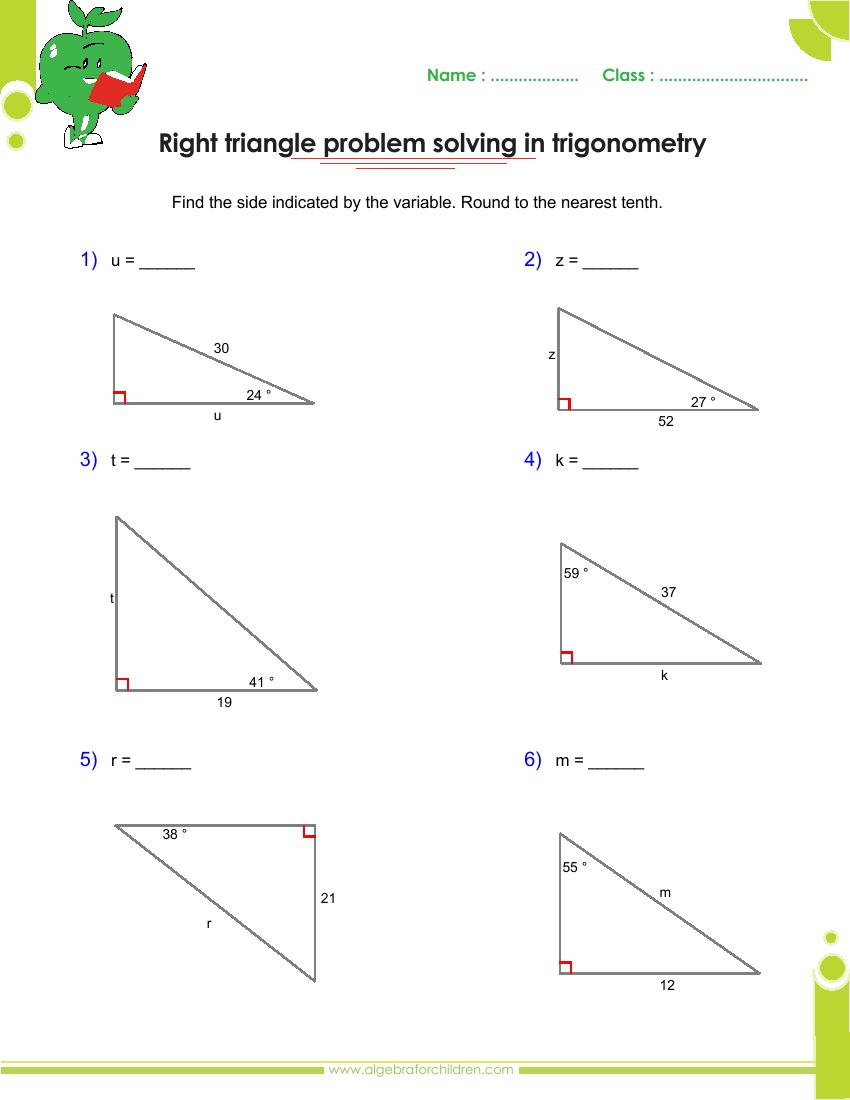
Image: www.e-streetlight.com
3. Tangent (TOA):
The tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. Imagine tangent as the “opposite” side over the “adjacent” side.
Navigating the Triangle: Finding Missing Sides
Now let’s see how these trigonometric ratios come into play when finding missing sides of a right triangle. Suppose you have a right triangle with one known side and one known angle (besides the right angle, of course). Armed with the SOH CAH TOA, you can solve for the missing side:
Example 1: Finding the hypotenuse
Imagine a right triangle with an angle of 30 degrees and a side opposite this angle measuring 5 units. To find the hypotenuse, we know the opposite side and are looking for the hypotenuse, so we use the sine function as it connects the opposite and hypotenuse.
-
sin(30°) = Opposite / Hypotenuse
-
sin(30°) = 5 / Hypotenuse
-
Hypotenuse = 5 / sin(30°)
-
Hypotenuse = 10 units
By using a calculator to find the sine of 30 degrees (which is 0.5), we can solve for the hypotenuse and determine it’s 10 units long.
Example 2: Finding the adjacent side
Now let’s change things up. Imagine a right triangle with an angle of 45 degrees and a hypotenuse measuring 8 units. We know the hypotenuse and want to find the adjacent side, so we’ll use the cosine function.
-
cos(45°) = Adjacent / Hypotenuse
-
cos(45°) = Adjacent / 8
-
*Adjacent = 8 cos(45°) **
-
Adjacent = 5.66 units (rounded to two decimal places)
Again, using a calculator to find the cosine of 45 degrees, we can determine the adjacent side is approximately 5.66 units long.
Unmasking the Angles: Finding Missing Angles
Just as we can use the trigonometric ratios to find missing sides, we can also use them to unveil the secrets of missing angles.
Example 1: Inverse Sine (arcsin)
Let’s say you have a right triangle with an opposite side of 2 units and a hypotenuse of 4 units. To find the angle opposite the side of 2 units, we’ll use the inverse sine function (arcsin) , which essentially “undoes” the sine function.
-
sin(θ) = Opposite / Hypotenuse
-
sin(θ) = 2 / 4
-
sin(θ) = 0.5
-
θ = arcsin (0.5)
-
θ = 30 degrees
Using a calculator, we find that the angle θ is 30 degrees.
Example 2: Inverse Cosine (arccos)
In another scenario, you have a right triangle with an adjacent side of 3 units and a hypotenuse of 5 units. To find the angle adjacent to the side of 3 units, we’ll use the inverse cosine function (arccos):
-
cos(θ) = Adjacent / Hypotenuse
-
cos(θ) = 3 / 5
-
cos(θ) = 0.6
-
θ = arccos(0.6)
-
θ = 53.13 degrees (rounded to two decimal places)
Using a calculator, we find the angle θ is approximately 53.13 degrees.
Example 3: Inverse Tangent (arctan)
Lastly, imagine a right triangle with an opposite side of 7 units and an adjacent side of 4 units. To find the angle opposite the side of 7 units, we’ll use the inverse tangent function (arctan):
-
tan(θ) = Opposite / Adjacent
-
tan(θ) = 7 / 4
-
tan(θ) = 1.75
-
θ = arctan(1.75)
-
θ = 60.26 degrees (rounded to two decimal places)
Using a calculator, we can determine the angle θ is approximately 60.26 degrees.
Mastering the Art: Tips and Tricks for Solving Right Triangles
Unlocking the secrets of right triangles isn’t about memorizing formulas – it’s about understanding the relationships between the sides and angles. Here are some tips and tricks to help you solve any right triangle problem with confidence:
-
Draw it out: Visualizing the problem by drawing the right triangle to scale can help you see the relationships between the sides and angles more clearly.
-
Know your ratios: Memorize SOH CAH TOA to easily recall which trigonometric ratio to use in each situation.
-
Use a calculator wisely: A calculator is a fantastic tool to find the values of sine, cosine, tangent, and their inverse functions.
-
Practice makes perfect: The more right triangles you solve, the more comfortable you’ll become with these trigonometric principles.
Right Triangle Trig Finding Missing Sides And Angles Worksheet Answers
Conclusion: Unlocking the Secrets Within
Right triangle trigonometry is a powerful tool that unlocks a world of possibilities. Whether you’re solving for missing sides, unraveling the mysteries of hidden angles, or exploring the real-world applications of this mathematical magic, understanding the principles of sine, cosine, and tangent will empower you to navigate the intriguing world of right triangles. So, grab your calculator, put on your thinking cap, and let the adventure begin! As you continue to explore the realm of right triangles, remember that the key to success lies in understanding the relationships between sides and angles, and practicing, practicing, practicing!





