Have you ever gazed at a magnificent cathedral window, awestruck by its intricate design? Or admired the symmetry of a snowflake, marveling at its delicate geometric patterns? These awe-inspiring structures, both natural and man-made, share a common thread – they are built upon the fundamental principles of geometry, specifically the study of polygons. Polygons are closed shapes made up of straight line segments, forming the very building blocks of our visual world. And within this fascinating realm lies the captivating concept of angles, which dictate the shape and form of these polygons.
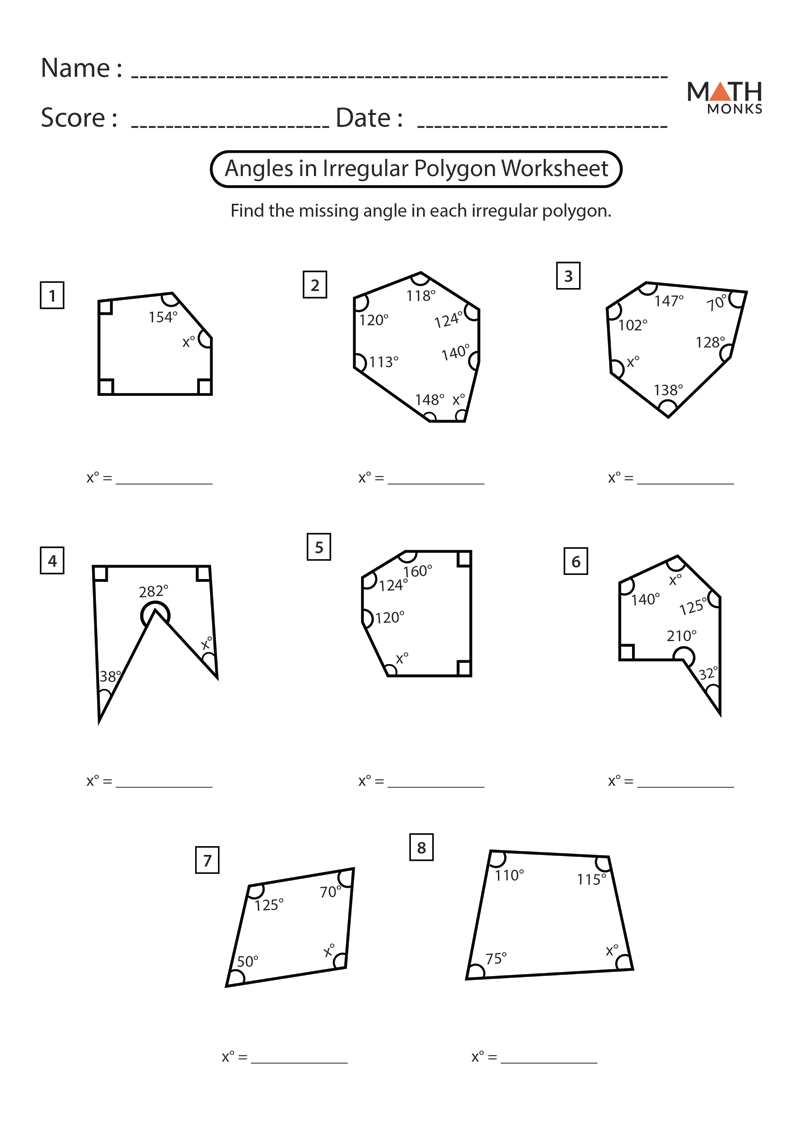
Image: materialcampusdelgado.z21.web.core.windows.net
Understanding how to calculate the angles of polygons is key to unraveling their secrets – a key that unlocks the door to deeper understanding and appreciation of the world around us. This is where the 6-1 Skills Practice Angles of Polygons Answer Key emerges as a valuable companion, guiding us through the intricacies of angle calculations and empowering us to confidently analyze and even design our own geometric wonders. So, let’s embark on an illuminating journey to uncover the secrets of polygons and their captivating angles!
Navigating the World of Polygons and Angles
Polygons, those fascinating shapes formed by straight line segments, hold a special place in the world of geometry. From the simple triangle to the complex decagon, each polygon possesses a unique character defined by its number of sides and, importantly, its angles.
Within each polygon, we find a set of interior angles that contribute to its overall shape. These angles are formed by the intersection of two sides, creating a space between them. The sum of these interior angles reveals a fascinating truth: it’s always predictable and consistent for any given polygon.
Imagine a humble triangle – the most basic polygon. Its three angles, when added together, always equal 180 degrees. This simple truth holds the key to understanding more complex polygons.
Unraveling the Secrets of Angle Calculations
One of the most fundamental concepts in understanding polygons is the formula to calculate the sum of their interior angles. This formula acts as a master key, unlocking the secrets of any polygon’s angles.
The formula is: *(n – 2) 180**, where ‘n’ represents the number of sides of the polygon.
Let’s break down this formula:
- (n – 2): This part signifies how many triangles can be formed within the polygon. For a triangle, we can only form one triangle (3 – 2 = 1). A quadrilateral can be divided into two triangles (4 – 2 = 2), and so on.
- 180: Each triangle has 180 degrees, and the formula multiplies this value by the number of triangles within the polygon.
Applying this formula allows us to calculate the sum of the interior angles of any polygon. For instance, for a hexagon (6 sides), the sum of interior angles would be (6 – 2) * 180 = 720 degrees.
The 6-1 Skills Practice Angles of Polygons Answer Key: Your Guide to Mastery
The 6-1 Skills Practice Angles of Polygons Answer Key serves as your dedicated guide, providing solutions to practice problems and aiding in your journey to mastery. It’s an invaluable resource, offering step-by-step solutions that demystify each problem and enhance your understanding of the concepts.
Let’s dive into the 6-1 Skills Practice Angles of Polygons Answer Key and explore a few key problem types:
- Finding the sum of interior angles: This type of problem involves applying the formula directly, using the given number of sides to calculate the sum of interior angles.
- Determining missing angles: These problems require you to use the sum of interior angles formula to calculate a specific angle, incorporating information about known angles or side lengths.
- Identifying polygon types: These problems present you with a set of angle measurements and challenge you to identify the type of polygon based on the sum of those angles.
Each problem presents a unique challenge, testing your understanding of various aspects of polygon calculations. By tackling these problems with the guidance of the 6-1 Skills Practice Angles of Polygons Answer Key, you gain invaluable experience and solidify your understanding of the concepts.
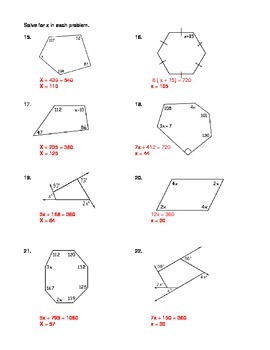
Image: worksheets.clipart-library.com
Mastering the Art of Geometry: Unveiling Applications
Understanding angles of polygons transcends the realm of theoretical knowledge; it finds practical applications across various fields. Architects rely on these principles to design stable and aesthetically pleasing structures. Engineers utilize them to optimize the strength and efficiency of bridges and other infrastructure. Artists and designers employ them to create captivating visual compositions.
The concept of polygons and angles is embedded in the very fabric of our world, influencing the shapes we see and the structures we create. By grasping the fundamentals of these concepts, we equip ourselves with a unique perspective, allowing us to see the world through a geometric lens.
6-1 Skills Practice Angles Of Polygons Answer Key
A Call to Action: Take the Leap into Geometry
As you embark on your journey through the fascinating world of polygons and angles, embrace the challenge with an open mind and a spirit of discovery. The 6-1 Skills Practice Angles of Polygons Answer Key is a valuable tool to accompany you on your path to mastery.
The more you practice and explore, the deeper your understanding will become.
Don’t be afraid to experiment, to delve deeper into the world of geometry, and to discover the endless possibilities that arise when you unlock the secrets of polygons and their angles. This journey of exploration will not only enhance your academic understanding but also deepen your appreciation for the beauty and elegance that exists in the world around us.





